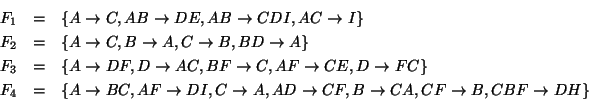Bases de Datos
Práctico 4: Dependencias Funcionales y Cubrimientos
G. Saiz - N. Wolovick
- Probar, sin utilizar los aximas de Amstrong, las reglas de inferencia adicionales sobre dependencias funcionales:
- Unión.
- Descomposición.
- Pseudotransitividad.
- Dado el siguiente conjunto de dependencias funcionales
encontrar, si es posible, una secuencia de derivación aplicando los axiomas de Amstrong para
las siguientes dependencias:
-
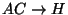
-
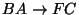
-
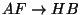
-
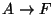
- Pruebe o niegue con un contraejemplo que las siguientes reglas de inferencia son válidas para una relación
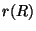 , con
, con
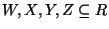 .
.
-
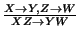
-
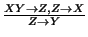
-
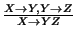
-
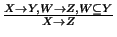
-
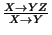
- Sea
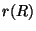 una relación. Probar que
una relación. Probar que 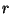 satisface
satisface
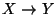 sii
sii 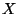 es una clave de
es una clave de 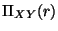 .
.
- Probar que los axiomas de Amstrong son independientes, es decir, no hay un subconjunto propio del cual se puedan probar
los restantes.
- Sea
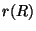 una relación. Probar que si
una relación. Probar que si 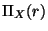 tiene la misma cantidad de tuplas que
tiene la misma cantidad de tuplas que 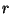 , entonces
, entonces 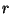 satisface
satisface
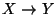 para todo
para todo 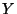 incluido en
incluido en 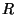 .
.
- Sea
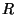 un esquema de relación y
un esquema de relación y 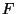 un conjunto de dependencias funcionales.
Dar una cota del número de dependencias funcionales en
un conjunto de dependencias funcionales.
Dar una cota del número de dependencias funcionales en 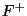 en base al número de atributos de
en base al número de atributos de 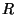 .
.
- Dados los siguientes conjuntos de dependencias funcionales
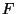 y
y 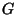 , decidir si son equivalentes.
, decidir si son equivalentes.
- Encuentre un cubrimiento no redundante para
- Dado
- Encuentre un conjunto de dependencias equivalente no redundate y reducido.
- ¿Es
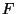 minimal? Si no lo es, encuentre un minimal equivalente.
minimal? Si no lo es, encuentre un minimal equivalente.
- ¿Es correcto el siguiente algoritmo?

- Para los siguientes conjuntos de dependencias funcionales, encuentre un conjunto equivalente minimal reducido
y un cubrimiento canónico.
- Dar conjuntos de dependencias funcionales que cumplan:
- No redundate, pero que no sea reducido.
- No redundante, pero no mínimo.
- Reducido no mínimo.
- Mínimo pero no reducido.
- Mínimo y reducido, pero hay algún cubrimiento equivalente que usa menor cantidad de símbolos.
bdd@hal.famaf.unc.edu.ar
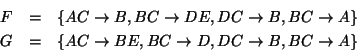
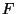 minimal? Si no lo es, encuentre un minimal equivalente.
minimal? Si no lo es, encuentre un minimal equivalente.