Dar planificaciones
- Una planificación SR.
- Un deadlock.
- Dar una transacción bien formada pero no en dos fases y otra que no esté bien formada, pero si sea de dos fases.
-
Demuestre que si
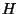 no está bien formada o no es dos fases, entonces es posible escribir una
transacción bien formada y en dos fases que produzca una planificación no serializable.
Siempre supondremos que se cumple con la propiedad
no está bien formada o no es dos fases, entonces es posible escribir una
transacción bien formada y en dos fases que produzca una planificación no serializable.
Siempre supondremos que se cumple con la propiedad 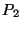 .
.
¿Cuántos historias
La relación
if
¿Este método sufre de deadlock? ¿Y de livelock? Respalde su respuesta con pruebas o contraejemplos.
decidir cuando y cuales de las cuatro transacciones aborta (si es que alguna lo hace) teniendo en cuenta que el planificador es
|
|
|
|
| read(A) | ||
| write(A) | ||
| write(A) | ||
| write(A) |
- En una historia
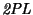 , se define el punto de lock de
, se define el punto de lock de 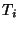 cuando se han tomado
todos los locks y no se ha soltado ninguno.
Demuestre que si
cuando se han tomado
todos los locks y no se ha soltado ninguno.
Demuestre que si
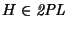 entonces
entonces
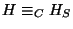 donde el orden de
donde el orden de 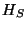 es
el de los locked points.
es
el de los locked points.
- Demuestre que
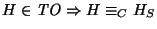 donde el orden de
donde el orden de 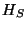 está dado por
está dado por
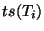 .
.
Suponga que usamos un detector de deadlocks que encuentra todos los ciclos elementales del
![]() y
rompe cada uno de esos deadlocks parciales abortando una víctima en el ciclo.
Demuestre que esto rompe todos los ciclos del
y
rompe cada uno de esos deadlocks parciales abortando una víctima en el ciclo.
Demuestre que esto rompe todos los ciclos del
![]() .
.