Pedro R. D'Argenio

Introduction

Computers have changed our lives forever. Three decades ago, the use of computer systems was reduced to specialised environments. The computational power of the system that put the first man on the moon was smaller than the computational power of a modern VCR. Nowadays, our interaction with some kind of computational-based device is just unavoidable. According to R.H. Bourgonjon (1998), the number of microprocessors that we encounter daily in our lives has increased from 2 in 1985 to 50 in 1995. We find these microprocessors in consumer electronics --such us TV's, VCR's, CD players--, transportation systems --including airplanes and air traffic control, cars, railway systems--, telecommunication systems, industrial plants, computer networks, medical equipment, . . . You name it! The malfunction of any of these systems has a variety of consequences ranging from simply annoying to life-threatening ones. For many of such systems, it is crucial that they provide a correct and efficient service. In order to gain confidence that such devices satisfy our standards of service, it has been recognised that formal analysis has to be carried out as part of their development.

Formal methods provide mathematically-based languages, techniques and automated tools for specifying and verifying this kind of systems (Clarke and Wing, 1996). They have proved to be a powerful and effective tool. Examples of their application abound. Areas in which they were successfully applied include consumer electronics (e.g. Helmink et al., 1994; Bengtsson et al., 1996b; Romijn 1999), hardware (e.g. Barret, 1989; Boyer and Yu, 1996; O'Leary et al. 1999), automobile industry (e.g. Ruys and Langerack, 1997; Lindahl et al., 1998), aerospace industry (e.g. Eastbrook et al., 1997; Crow and Di Vito, 1998), and weather catastrophe prevention (e.g. Kars, 1998).

Although originally focussed on software specification, the advance in formal methods is such that, nowadays, they provide support for every stage of the life cycle of system engineering, including testing (e.g. Tretmans, 1992; Heerink, 1998; Springintveld et al., 1999), and maintenance (e.g. Bowen et al., 1993; and van Zuylen, 1993).

In this dissertation we concentrate on the study of formal methods for the design phase of the life cycle of system engineering.

In the formal analysis of systems, there are several aspects that should be taken into account:

• Control. The basic aspects of a design is to obtain a correct control flow, i.e., a suitable causal dependency between events. The temporal order in which events happen is crucial for the correctness of a system. For instance, it is evident that a buffer must first accept an input in order to produce an output. The control aspects are essential in the analysis of systems and cannot be overlooked.
• Data. Many systems strongly rely on data manipulation. Data usually determines the control flow of the system. Sometimes, data consistency is in the main interest of the system under consideration (e.g. databases). Some other systems, such as many protocols, do not rely heavily on data and can be abstracted in the formal analysis.
• Time. A timed system is a system whose behaviour is constrained by requirements concerning the occurrence of events with respect to (real) time. These timing conditions may speak about the acceptable performance of the system or a deadline that should be met.

In this thesis we study and develop formalisms for the design and analysis of systems in which time is an important factor.

1  Real-Time Systems

Most of the systems we encounter in our daily life require real-time interaction. For example, when we withdraw money from a cash dispenser, we expect the machine to react within a reasonable amount of time. But our patience has limits and if the transaction delays more than expected, we feel annoyed. For some other systems, it has far more critical consequences if they do not react on time. For instance, a gate controller in a rail-road crossing must react within a very specific period of time when a train is approaching, and close the gate. A small delay could cause a collision with fatal consequences.

In these two examples, we can clearly differentiate between two classes of real-time constraints: those that require that a system must react in time, and those that it should react in time but occasionally may not. If a system belongs to the first category it is referred to as a hard real-time system, if it belongs to the second one, as soft real-time system.

The analysis of hard real-time systems requires a full exploration of its behaviour searching for undesirable situations. The violation of a timing requirement is unacceptable. Notice the absolute characteristics of the judgment. There are only two options: a system is correct or not. For instance, the rail-road crossing system must satisfy the safety property stating that it is always the case that, if a train is in the crossing, then the gate is closed. The act of formally analysing whether a system satisfies a property or not, is known as verification.

In contrast, the analysis of soft real-time systems requires a parameter of adequacy. For instance, we find it reasonable that at least 95% of the times we withdraw money, the cash dispenser does not make us wait. The soft real-time requirements are typically concerned with the performance characteristics of systems and are usually related to stochastic aspects of various forms of time delay, such as, for example, mean and variance of a message transfer delay, service waiting times, etc. In addition, a stochastic study of the system also allows for reliability analysis, such as, average time during which the system operates correctly. Nevertheless, not all the parameters are soft. Some requirements still must be satisfied. After all the cash dispenser should eventually react by delivering our withdrawal or reporting that it is out of order.

The contribution of this dissertation is divided in two parts. The first part focuses on the development of a formal language for the specification of hard real-time systems built on top of existing theory. In the second part, we develop a formal framework for the specification and analysis of soft real-time systems.

Since the characteristics of the information we want to collect from soft real-time system is stochastic, we also refer to these systems as stochastic systems. For simplicity, we refer to hard real-time systems as timed systems.

2  Algebras and Automata

Probably the simplest way to represent behaviour is by means of automata. An automaton is a graph containing nodes and directed, labelled edges. Nodes represent the possible states of a system and edges (or transitions) represent activity by joining two nodes: one being the source state, that is, the state before "executing" the transition, and the other, the target state, which is the state reached after executing the transition. A simple and self-explanatory example is given in Figure 1.

Figure 1: An example of an automaton
 

Automata have been extended in many forms and used for many purposes, including testing (e.g. Chow, 1978;Tretmans, 1992; Heerink, 1998), programming language semantics (e.g. Plotkin, 1981; Winskel, 1993), model checking (e.g. Clarke and Emerson, 1981; Queille and Sifakis, 1982) and many other forms of verification. All these techniques provide a solid mathematical framework for the validation of systems. For instance, in model checking, the requirements are expressed by formulas in an appropriate logic and they are checked to be satisfied by the automaton that models the possible behaviours of a system. Such a satisfaction relation is a well defined mathematical relation. Alternatively, verification can be carried in terms of semantic relations over automata. That is, both the requirements and the system are specified by automata, the first one being usually simpler, and they are checked to be related by an equivalence or a preorder relation. Such a relation represents the "implementation" or "conformance" relation. Examples include language inclusion (Hopcroft and Ullman, 1979), failure semantics (Brookes et al., 1984), and bisimulation (Milner 1980).

The process of specification is the act of writing things down precisely. The main benefit in doing so is intangible--gaining deeper understanding of the system being specified. It is through this specification process that developers uncover design flaws, inconsistencies, ambiguities, and incompleteness (Clarke and Wing 1996). Although automata give a nice graphic representation of the system we want to describe, this same characteristic turns specifications unwieldy as the model gets larger and more detailed.

In order to specify complex systems we need a structured approach, a systematic methodology that allows us to build large systems from the composition of smaller ones. Process algebras were conceived for the hierarchical specification of systems. A process algebra is an algebra as it is understood in mathematics that is intended to describe processes. Each element of the process algebra represents the behaviour of a system in the same way as an automaton does. In addition, a process algebra provides operations that allow to compose systems in order to obtain more complex systems. Typical examples of these operations are the sequential composition and the parallel composition. For instance, if p and q represent two systems, we can compose them in parallel to obtain a larger system p||q. Notice that the behaviour modelled by this operation can be complex, but this is hidden behind the simple expression p||q.

As any algebra, a process algebra satisfies axioms or laws. The interest of having an axiomatisation for a process algebra is two-fold. First, the concept of algebra is fundamental in mathematics. Therefore, the given axiom system will help to understand the discussed process algebra and the concepts it involves. Second, the analysis and verification of systems described using the process algebra can be partially or completely carried out by mathematical proofs using the equational theory.

The works of Hoare (1978) and Milner (1980) marked the origin of the process-algebraic approach that led to a new broad research area.

In this thesis we introduce and study process algebras and automata for the design and analysis of hard and soft real-time systems.

Algebras and Automata for Timed Systems

Several models for the analysis and specification of timed systems have been devised, including timed Petri-nets (Sifakis, 1977), duration calculus (Chaochen et al., 1991), and a variety of extensions of automata with time information (e.g. Lynch and Vaandrager, 1996; Segala et al., 1998; Lynch et al., 1999).

A model that has been accepted with a large success is timed automata (Alur and Dill, 1990, 1994; Henzinger et al., 1994). Inherently, a timed system induces an infinite behaviour due to the need of representing dense time. Timed automata propose a symbolic way to describe this infinite behaviour. In so doing, it enables a full state space exploration by traversing a "symbolically finite" state space. This is mainly the reason for the popularity of this model.

Timed automata have served as a model for many model checking algorithms (e.g. Alur et al., 1993; Henzinger et al., 1994; Yovine, 1993; Yi et al., 1994; Olivero, 1994; Petterson, 1999) and tools that implement these algorithms such as Kronos (Daws et al., 1996; Bozga et al., 1998), Uppaal (Bengtsson et al., 1996b; Larsen et al., 1997), and HyTech (Henzinger et al., 1995). These tools were used in a diversity of case studies (e.g. Ho and Wong-Toi, 1995; Daws and Yovine, 1995; Bengtsson et al., 1996a; Maler and Yovine, 1996; D'Argenio et al., 1997; Lindahl et al., 1998). Timed automata were also extended to study hybrid systems (Alur et al., 1995) and served as a model for a theory of timed test derivation (Springintveld et al., 1999).

A process algebraic approach for timed systems has also been pursued. Originally, time was included in a discrete fashion (e.g. Groote, 1991; Moller and Tofts, 1990; Hansson, 1994; Nicollin and Sifakis, 1994; Baeten and Bergstra, 1996; Vereijken, 1997), that is, time is represented as a "tick" action that describes the passage of a single time unit. These process algebras are adequate to model digital systems but they cannot describe real-time systems in a natural way. For this reason, dense time process algebras were developed (e.g. Yi, 1990, 1991; Baeten and Bergstra, 1991; Davies et al., 1992; Klusener, 1993; Leduc and Léonard, 1994).

Some of these process algebras have been formally related to timed automata (e.g. Nicollin et al., 1992; Fokking, 1993; Bradley et al., 1995; see also Section 5.8). However, these relations only provide a semantic connection and none of them is complete in the sense that such a connection is bijective. Languages that completely represent timed automata have been defined (Lynch and Vaandrager, 1996; Alur and Henzinger, 1994; Yi et al., 1994; Pettersson, 1999) but none of them provide an algebraic framework. To our knowledge no axiomatic theory of timed automata has been devised until now.

Algebras and Automata for Stochastic Systems

The analysis of stochastic systems has received a lot of attention but, traditionally, outside the community of formal methods. Long ago, mathematicians defined models for the analysis of stochastic processes. These models, which include the so-called continuous time Markov chains, were used to analyse the performance of systems. But systems started to become more complex and there was a need for a more sophisticated notation to specify performance models. This led to the definitions of models such as queueing networks (Kleinrock, 1975; Harrison and Pattel, 1992) and a diversity of stochastic Petri-nets (Ajmone-Marsan et al., 1995).

Models based on continuous time Markov chains represent the timing of events as a stochastic variable distributed only according to an exponential distribution. This restriction is the key for the vast analytical and numerical theory that supports continuous time Markov chains. However, restricting to exponential distributions is often not realistic and may lead to results that are not sufficiently accurate. For instance, in the analysis of high-speed communication systems or multi-media applications the correlation between successive packet arrivals tends to have a constant length; therefore, the usual Poisson arrivals and exponential packet lengths are no longer valid assumptions (Brinksma et al., 1995). More general models, such as generalised semi-Markov processes (Whitt, 1980; Glynn, 1989; see also Cassandras, 1993; Shedler, 1993), allow for the description of timings that may depend on any distribution.

Unfortunately, none of these models provides a suitable framework for the composition of distributed and communicating systems.

The formal methods community tackled the description and analysis of stochastic systems by means of so-called probabilistic process algebras (e.g. Giacalone et al., 1990; Hansson, 1994; van Glabbeek et al., 1995; Baeten et al., 1995; Andova, 1999; Baier, 1999), although initially it was intended for verification purposes rather than performance analysis. In addition, they only deal with discrete probability distributions, and most of them do not include a notion of time.

It was not until the seminal work of Ulrich Ferzog (1990) that process algebras and performance models were combined. Stochastic process algebras were thus introduced.

Taking advantage of the analytical framework provided by continuous time Markov chains, so-called Markovian process algebras were devised. They include TIPP (Hermanns and Rettelbach, 1994), PEPA (Hilston, 1996), EMPA (Bernardo and Gorrieri, 1998; Bernardo, 1999), MPA (Buchholz, 1994), and IMC (Hermanns and Rettelbach, 1996; Hermanns, 1998). The general approach, including any continuous distribution function, has also been addressed (Götz et al., 1993; Strulo, 1993; Harrison and Strulo, 1995; Brinksma et al., 1995; Katoen, 1996; Priami, 1996; Bravetti et al., 1998).

Each approach deals with the parallel composition in a different manner. When no interaction is involved, parallel composition can be easily defined in Markovian process algebras. If arbitrary distributions are allowed, this definition proved to be more complicated yielding complex or infinite semantic objects.

Synchronisation leads to more complicated decisions (see Hillston, 1994). Not all the process algebras provide a symmetric interaction. For instance, EMPA requires that at most one of the synchronising components is time dependent. The others must be "passive". The kind of synchronisation we are interested in is what Jane Hillston (1994) calls patient communication. A patient communication takes place when all the components that intend to synchronise, are ready to do it. This approach is adopted by Harrison and Strulo (1995); Brinksma et al. (1995); Hermanns (1998). Hillston's PEPA also uses this approach but needs to approximate the distribution of the time in order to stay in the domain of exponential distributions. Notice that patient communication can model the aforementioned asymmetric synchronisation: a passive process is always ready to synchronise.

Another issue that arises as a consequence of considering parallel composition in interleaving models (such as automata-based models) is non-determinism. Only Hermanns' Interactive Markov Chains (IMC) and Harrison and Strulo's process algebra deal with non-determinism in a satisfactory way¹. The rest of the process algebras solve non-determinism probabilistically,either by the so-called race condition, or by explicitly determining the branching probabilities.

3  Our Contribution

This dissertation consists of two parts. In the first part of the thesis we concentrate on timed systems. Timed automata is a well-established model for the analysis of hard real-time systems that has been used successfully on many occasions. However no algebraic theory of timed automata has been discussed so far. The main contribution of this part is thus a process algebra for timed automata which we call (read hearts). Its syntax contains the same "ingredients" as the timed automata model. Moreover, we provide an axiomatic theory that allows us to manipulate algebraically timed automata.

In the second part we concentrate on stochastic systems. Although many models have been successfully used for the analysis of performance and reliability of soft real-time systems, none of them provide a general and suitable model to represent systems compositionally. Based on generalised semi-Markov processes and timed automata, we define a new model which we call stochastic automata. The stochastic automata model is a general stochastic model that provides an adequate framework for composition.

Several stochastic process algebras have been introduced in the last decade. The most successful ones restrict to the so-called Markovian case. General approaches to stochastic process algebras followed a less successful path, mainly due to the lack of a suitable model to represent this general models in a compositional fashion.

Using stochastic automata as the underlying semantic model we define (read spades), a process algebra for stochastic automata. This stochastic process algebra considers arbitrary distributions and non-determinism. A particular characteristic is that parallel composition and synchronisation can be easily defined in the model, and it can be algebraically decomposed in terms of more primitive operations according to the so-called expansion law. We remark that this last property is not present in any of the other existing general stochastic process algebras.

In order to show the feasibility of the analysis of systems specified in , we report on algorithms and prototypical tools to study correctness as well as performance and reliability. The tools were used to analyse several case studies which are reported as well.

4  Outline of the Dissertation

This thesis is divided in four parts. The first one is intended to report the introductory concepts. It includes this chapter and Chapter 2 which contains the preliminaries. There, we introduce and discuss intuition and foundations of many aspects which are traditional to concurrency and process theory such as transition systems, bisimulation, process algebras, and properties of each one of them. Although the reader is assumed to have a background in concurrency theory, Chapter 2 intends to recall all those concepts that will be used and redefined in the context of timed and stochastic systems. Thus, intuition or the rationale behind traditional concepts are not repeated in the other chapters except when necessary.

The second and the third part discuss the timed and the stochastic theories respectively. They have been structured as follows

1. concrete semantic model,
2. symbolic semantic model,
3. syntax and semantics of the process algebra,
4. its equational theory, and
5. applications.

This structure is somehow present already in Chapter 2, although there, the concrete and symbolic model are the same and the last part has been omitted.

The contributions on timed systems are reported in the second part. It includes the following chapters:

Chapter 3.

We give a formalisation of timed transition systems. A notion of bisimulation for this model is defined.

Chapter 4.

The timed automata model is revisited. We adapt it to our framework and give semantics in terms of timed transition systems. Several notions of equivalences are defined and related.

Chapter 5.

, the process algebra for timed systems, is introduced. Its semantics is defined in terms of timed automata. Equivalences and congruences are discussed.

Chapter 6.

Several equational theories for are defined. We study their soundness and completeness with respect to the equivalences defined in Chapter 4 and use it to derive an expansion law.

Chapter 7.

We discuss several applications of including specification and analysis of timed systems, and algebraic reasoning of timed automata.

Some preliminary results of this first part have been published in (D'Argenio and Brinksma, 1996a,b; Dargenio, 1997a,b).

In the third part we report on our contributions to the specification and analysis of stochastic systems. It includes the following chapters:

Chapter 8.

We introduce probability transition systems that allow for arbitrary probability distributions and define a probabilistic bisimulation on this model.

Chapter 9.

Stochastic automata are introduced. We discuss different semantics in terms of probabilistic transition systems. Equivalences at the symbolic level are defined and related. We formally compare stochastic automata with generalised semi-Markov processes.

Chapter 10.

We introduce , a process algebra for the description of stochastic systems, and define its semantics in terms of stochastic automata. Congruence relations are discussed.

Chapter 11.

We study several axiomatisations and laws for and prove soundness and completeness with respect to the congruences reported in Chapter 10. An expansion law is derived from the equational theory.

Chapter 12.

We define the theoretical background of algorithms for the quantitative and qualitative analysis of specifications. We report on prototypical tools that implement those algorithms and discuss their use in a variety of case studies.

Some preliminary results of this part have appeared in the following articles: (D'Argenio et al., 1997a, 1998a,b,c, 1999b).

In Chapter 13 we give some concluding remarks and discuss possible directions for further research. There is also a fourth part that includes appendices containing the most involved technical details. Appendices A, B, and C report the proofs of theorems appearing in the second part, while Appendices E, F, and G contain the proofs of the third part. In Appendix D we recall some basic concepts of probability theory.

An overview of the chapter dependencies of this dissertation is given in Figure 2. Part two and three can be read in an independent fashion. Occasionally, part three will make a reference to the second part for the sake of not being redundant. This will be explicitly indicated.

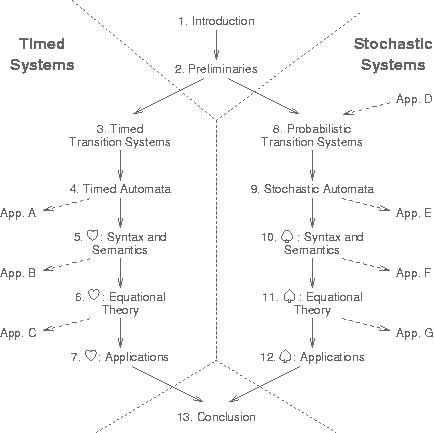
Figure 2: Schematic view of the dissertation

¹ EMPA considers non-determinism as well, but it was recently shown that it may violate compositional consistency (Bernardo, 1999).

Download the full thesis.